이 글은 Nikhita Singh Shiv Kalpana의 'Data Normalization With R'을 번역 및 정리한 글입니다. 원문은 여기서 찾으실 수 있습니다.
*맨 밑에 요약 및 정리가 있습니다.
#데이터 #정상화 #표준화 #Data #Normalization #Standardization #Z-score #Robust #Scalar # Min-Max #UnitLength #머신러닝 #Bioinformatics
데이터 분석에서 데이터 전처리 과정은 가장 중요한 단계 중 하나입니다. 프로그래머들은 종종 이 단계를 무시하거나 건너뛰고 바로 분석으로 들어가는데, 이것은 데이터에 편향을 줘서 예측 정확성에 영향을 주기도 합니다.

Data Normalization은 무엇인가요?
데이터 정상화(Data normalization)는 수치의 범위를 조정하여 표준 수치로 맞추는 자료 전처리 단계입니다. 머신러닝에서는 피쳐 스케일링(feature scaling)이라고도 합니다.
왜 Data Normalization이 필요한가요?
거리 기반 알고리즘(Distance-based algorithms) 및 기울기 강하 기반 알고리즘(gradient-descent-based algorithm) 등의 머신러닝 알고리즘은 자료의 범위가 맞춰져 있어야 합니다. 그 이유를 알아보기 위해 아래의 예를 같이 보겠습니다. 1.1년에서 10.5년까지 범위인 경력과 $37k에서 $122k까지 그에 상응하는 연봉의 두 변수를 가진 35명의 데이터가 있습니다 (출처: https://www.kaggle.com/rsadiq/salary)
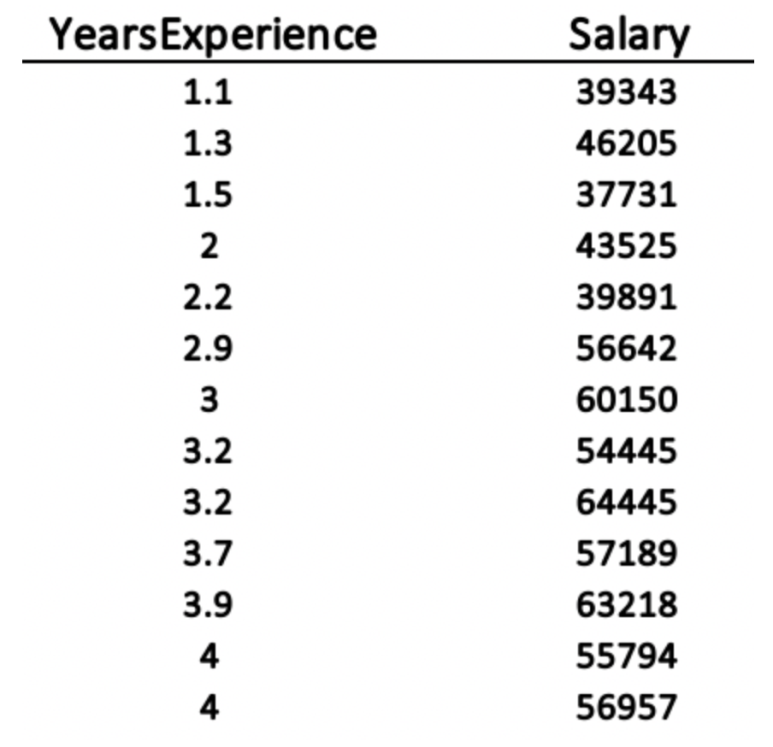
SVM, K-Means, KNN과 같은 거리 기반 알고리즘(distance-based algorithms)은 거리함수(distance function)를 이용하여 대상 간의 유사점을 찾아 구분합니다. 이러한 알고리즘은 변수의 크기에 민감합니다. 만약 범위를 동등하게 맞추지 않으면, 더 큰 범위의 변수인 연봉이 상대적으로 작은 변수인 경력에 비해 더 많은 영향을 가지는 것으로 판단하게 될 것입니다. 그리고 이것은 데이터에 편향을 가져와 결국 정확도에 영향을 미칩니다.
이와는 달리 기울기 강하 기반 알고리즘(gradient-descent-based algorithms)은 벡터 값으로 이루어진 함수 θ를 사용합니다. 변수들의 범위 서로 다를 때, θ는 범위가 작은 변수에서 그 학습 속도가 더 빠르기 때문에 더 빨리 강하합니다. 그러므로 변수들이 같은 학습 속도를 가진 채로 움직이도록 조정할 필요가 있습니다. 그리고 이것이 최소값에 더 빠르게 수렴하도록 만들죠. 이 현상은 아래의 그래프에서 관찰할 수 있습니다. 왼쪽 그래프는 범위 조정이 되지 않아서 (작은 범위의 변수가 더 느린 학습 속도를 가지기 때문에) 범위 조정이 된 오른쪽의 그래프보다 더 시간이 많이 걸립니다.

주성분 분석(Principal component analysis; PCA)은 최대의 분산을 포착하려함으로 범위 조정이 필요합니다. 만약 범위가 조정되어있지 않다면, 더 큰 범위를 가진 변수가 다른 변수들에게 영향을 미치는 편향이 생길 수 있습니다.
나무 기반 모델(Tree-based models)은 회귀와 분류에 특정한 규칙을 따릅니다. 그러므로, 여기서는 범위 조정이 필요치 않습니다.
Data Normailzation의 방법들
1. Z-score Normalization (Standardization; 표준화)
2. Robust Scalar
3. Min-Max Normalization
4. Mean Normalization
5. Unit Length
Z-score Normalization (Standardization)
Z-score normalization은 각 관측치 x에서 표본 평균을 뺀 후, 그것을 표준 편차로 나눈 x'를 다룹니다. 이러한 x'의 평균과 표준편차는 각각 0과 1이 됩니다. 공식은 다음과 같습니다:



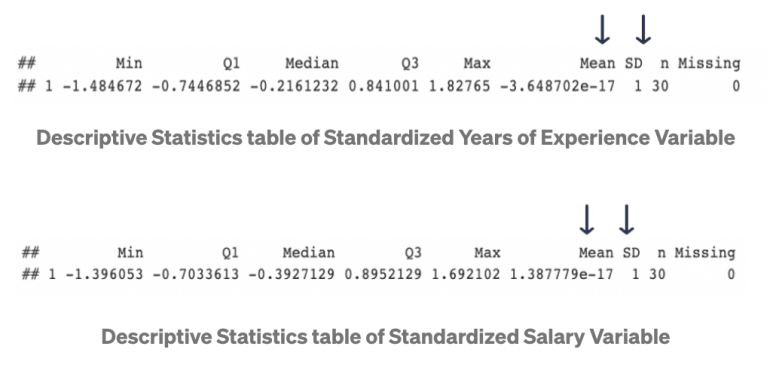
위의 데이터 분포 설명에 보이듯이, 변수 표준은 0에 근접하고 표준편차는 1이 됩니다. 또한, 최소값과 최대값은 수치 범위를 벗어납니다. 표준화(Standardization)가 범위 제한을 하진 않지만, 표본 평균과 표준편차는 여전히 이상치(outlier)에 영향을 받습니다. 이러한 이상치(outlier)가 있을 때에는, Robust scalar 방식을 쓰는 것이 좋습니다.
Robust Scalar
바로 위에서 언급한 것처럼, Robust Scalar는 이상치(outlier)가 있을 때에 사용할 수 있습니다.
Robust scalar는 원래 값인 x에서 중간값(median)을 뺀 다음, 1사분위와 3사분위 사이의 범위인 사분위수 범위(interquarile range)로 나눠주어 x'로 변환시킵니다. 그 공식은 다음과 같습니다:
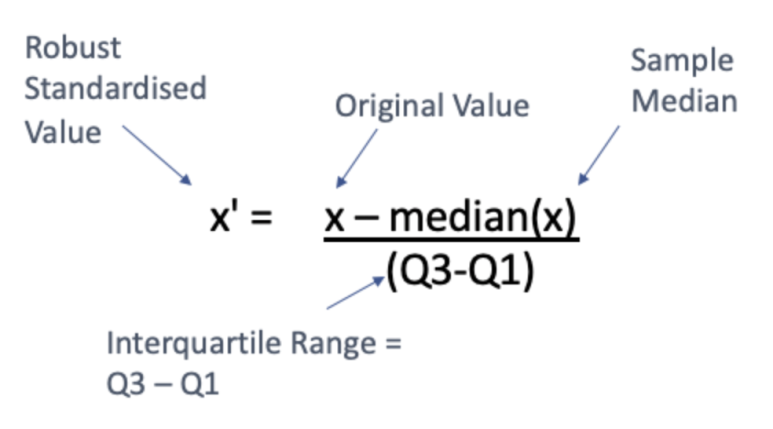



데이터 분포 설명에서 보이듯이, 중간값(median)은 0이 됩니다. 또한, 평균과 표준편차는 0과 1이 아닙니다. 적용 후 최소값과 최대값 또한 제한되지 않습니다.
Min-Max Normalization
Min-Max normalization은 모든 x 값을 0과 1사이의 값으로 변환하며, 이것은 (0-1) normalization으로 불리기도 합니다. 만약 데이터가 음수 값을 가지면, 수치 범위는 -1에서 1 사이로 지정합니다. Min-max normalization의 공식은 다음과 같습니다:
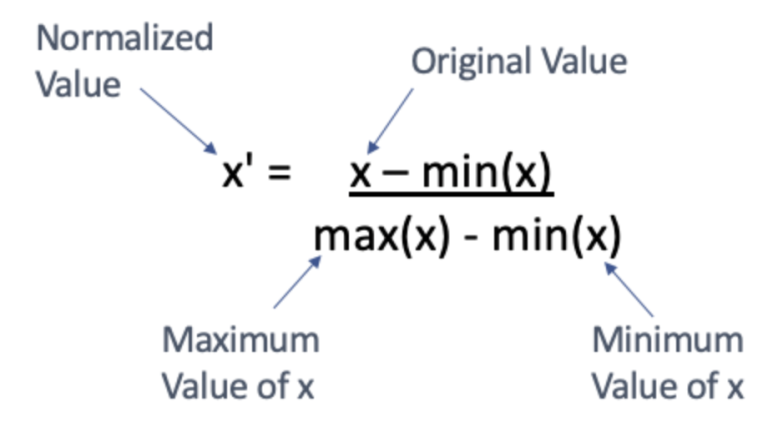
정해진 0과 1사이가 아니라 특정한 [a, b] 간격으로 범위 조정도 가능합니다. 이러한 방법은 예를 들어 최대값이 255이고 최소값이 0을 가진 픽셀의 이미지 처리에 쓰입니다. 공식은 다음과 같습니다:
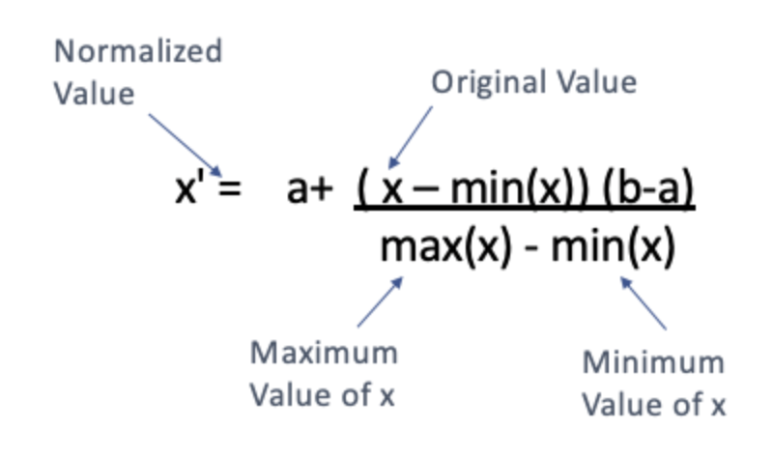

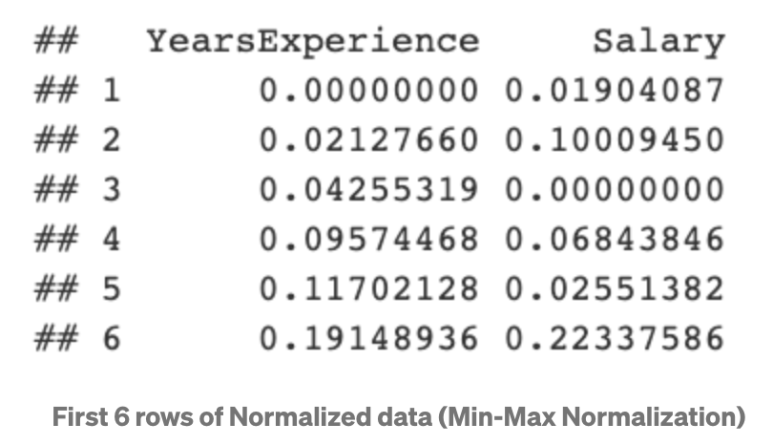

위의 분포에서 보는 것과 같이, Min-max normalization을 적용한 수치의 최소값은 0, 최대값은 1이 됩니다. 모든 수치는 이 사이에서만 존재합니다.
Mean Normalization
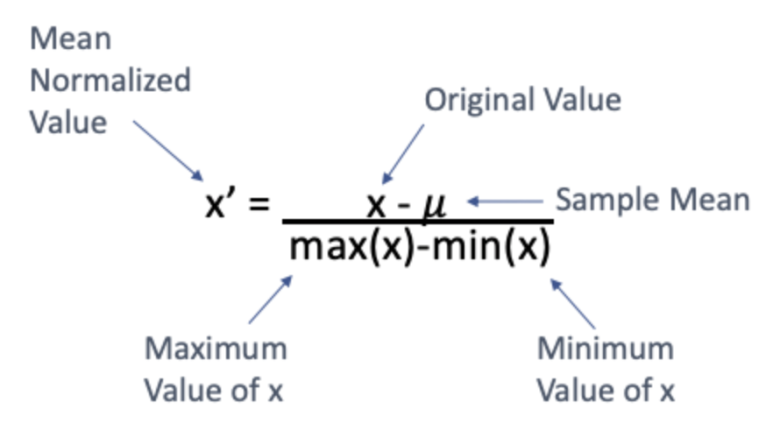
Mean normalization은 Min-max normalization과 같은 방식으로 수치를 변환시킵니다. 한가지 다른 점은 먼저 모든 값 x에 표본 평균을 뺀다는 점입니다. 공식은 다음과 같습니다:

Unit Length Normalization
Unit length normalization은 각각의 x 벡터를 유클리드 길이(Euclidean length)로 나누어서 변환시킵니다.
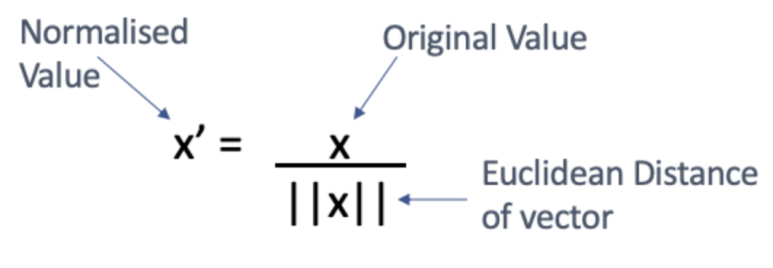

Min-max normalization과 Unit length는 둘 다 범위가 [0,1]로 제한됩니다. 이것은 만약 데이터에 이상치(outlier)가 있다면 큰 단점입니다. 이상치가 있는 데이터는, Robust scalar 방법을 사용합니다.
Scatter Plot
이제 산점도(scatter plot)을 그려서 normalization 이전과 이후의 데이터를 비교해 보겠습니다. 원래의 데이터를 그리는 코드는 다음과 같습니다:

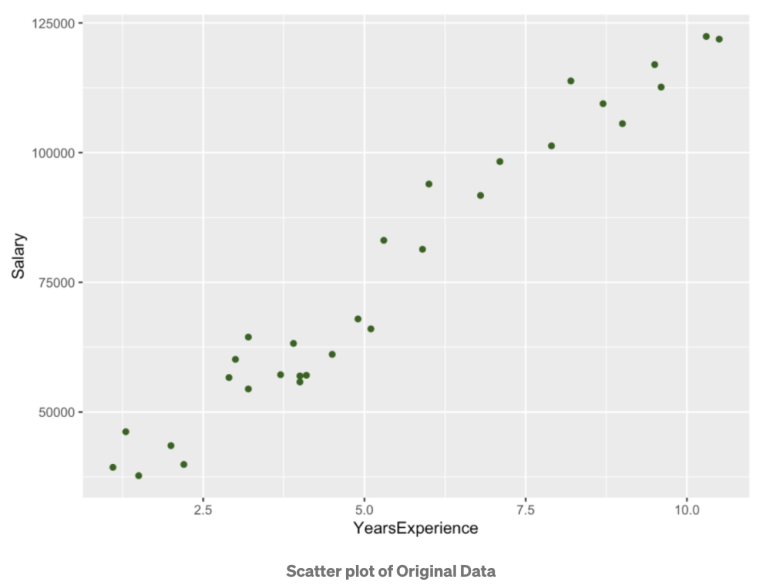
이제 normalization을 적용한 산점도를 그려보겠습니다.

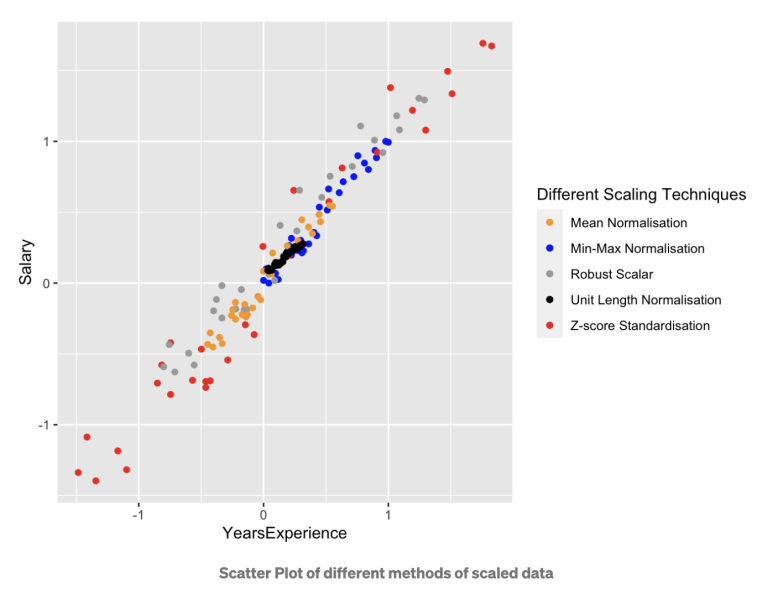
원래의 데이터와 Normalization을 적용한 데이터의 분포에서 볼 수 있듯이, 연봉과 경력 년수 두 변수 사이의 관계 및 데이터의 분포에는 변화가 없습니다.
Normalization vs. Standardization
가장 널리 쓰이는 normalization 방법은 min-max normalization과 standardization입니다. 이 둘을 비교해보겠습니다.

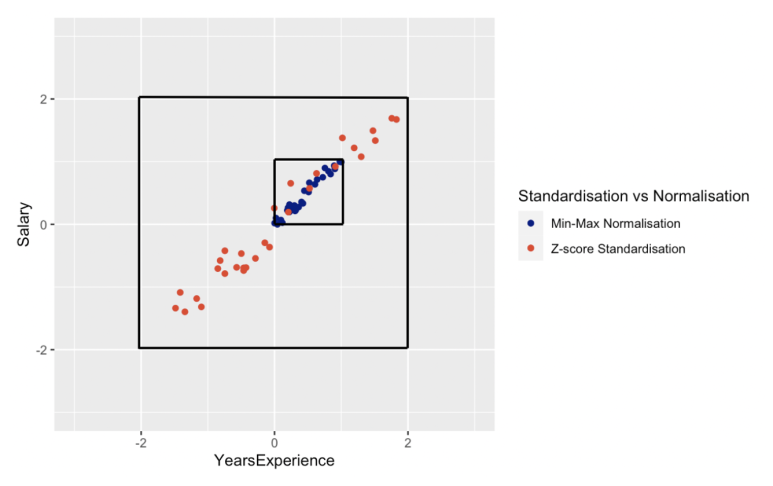
위의 그래프에서 보이듯, min-max normalization은 수치들이 0과 1사이인 반면에 standardization의 수치들은 0-1 범위를 벗어납니다.
Normalization vs. Standardization을 KNN 알고리즘에 적용한다면?
이러한 normalization 방법들을 KNN과 같은 머신러닝 알고리즘에 적용해 보겠습니다.

두 방법을 비교하기 위하여 평균 제곱근 오차(root mean square error; RMSE)를 각각 계산해보았습니다. RMSE가 낮을 수록, 모델이 더 잘 맞는다는 의미입니다. 아래의 표에서 보이듯, normalization을 거치지 않은 데이터는 아주 큰 RMSE를 가집니다. 또한, min-max normalization이 KNN 알고리즘에서는 더 나은 결과를 가져오는 것도 알 수 있습니다.

어떠한 Normalization 방법을 선택할 지는 어려운 질문입니다. 하지만, 이 질문에 정답은 없습니다. 아주 많은 경우에, 우리가 어떠한 질문을 던지느냐에 따라서 방법의 선택이 결정될 수 있습니다.
요약 및 정리:
1. 0-255 사이의 픽셀값을 가지는 이미지 처리와 같이 특정한 범위 내로 표준화를 해야한다면 min-max normalization을 사용합니다.
2. 데이터가 평균을 중심으로 분포하길 원한다면, 그리고 표준편차가 1로 동일하길 원한다면, Z-score standardization을 사용합니다.
3. 데이터의 분포를 모르고, 데이터가 가우시안 분포(Gaussian distribution)를 따르지 않는다면, min-max normalization을 사용합니다.
4. 데이터가 가우시안 분포를 따른다면, standardization을 사용합니다.
'Statistics and Probability' 카테고리의 다른 글
| [MDF]확률과 통계의 기본개념 (0) | 2013.11.26 |
|---|---|
| Metropolis-Hastings algorithm (0) | 2012.12.07 |
| Bayes Factor (베이즈요인) (0) | 2012.08.03 |
| 모델 선택 (Model Selection) (0) | 2012.08.03 |
| 지수분포 (Exponential distribution) (1) | 2012.07.20 |








